

Decision-support systems demand speedy access to data, no matter how complex the query--or the data. To answer the call may require increasingly exotic indexing methods
Speeding access to data is often a critical concern for relational DBMS programmers and administrators. The proliferation of end user-oriented query tools, the availability of sophisticated applications for relational DBMSs, and the growing interest in data warehousing and online analytical processing (OLAP) applications has contributed to the complexity of workloads that today's databases must support.
Uppermost in the minds of many database professionals is the issue of performance. Indexes offer one way to speed data access, and during the past several years many vendors have improved their indexing technology or offered new types of indexes to cope with users' changing workloads.
Among the types of indexes supported or under exploration by commercial DBMS vendors are B+ trees, bitmap indexes, join indexes, and R-trees. Each differs in implementation and target use, but each offers the potential to improve query performance for different applications. Of course, a number of other factors can also be critical for meeting performance goals, such as optimization techniques, memory management, concurrency control mechanisms, and tuning options. Nonetheless, indexing technology can also play a key role, and for this reason it's important to understand the fundamentals of some of the commercially available indexing techniques, as well as the types of queries for which each might be best suited.
This article explores the fundamentals of B+ trees (useful for general database and decision-support applications), bitmap and join indexes (often targeted to support multidimensional analysis), and R-trees (designed for queries involving spatial data). Information about each is presented in its simplest form to illustrate the basic differences among them. On occasion, specific implementation examples refer to commercial products.
WHY USE INDEXES?
Like an index in a book, indexes in a DBMS can provide one relatively quick
means of locating data of interest. This is particularly important in RDBMSs,
which do not use a navigational-based approach to data access. Because the
DBMS must determine the most efficient means to resolving a user's request,
it is helpful when a variety of data access paths are made available, including
appropriately defined indexes.
Without indexes, the DBMS may be forced to conduct a full table scan (reading every row in the table) to locate the desired data, which can be a lengthy and inefficient process. Although hashing is useful for random, single-row retrieval, it is best avoided for multirow requests, including range searches and requests for sorted rows. Indexed scans are much more efficient than searches of database tables because index entries are generally much shorter than stored rows. Many more index entries than rows can be stored on a single page. Thus, using an index achieves considerable reduction in the amount of I/O processing needed to locate the desired data.
However, creating indexes requires careful consideration. Although indexes
can be quite useful for speeding data retrieval, they can slow performance
of database writes. This slowdown occurs because a change to an indexed
column actually requires two database writes-one to reflect a change in
the table and one to reflect a corresponding change in the index. Thus,
if the activities associated with a table are primarily write-
intensive, it's important to make judicious use of indexes on the relevant
tables. Indexes also require a certain amount of disk space, which must
be considered when allocating resources to the database.
B+ TREES
The major relational DBMS vendors, including IBM, Oracle, Sybase, and Tandem,
offer products that support B+ tree indexes (or a close derivative). Such
indexes can be defined on one or more columns in a table to help facilitate
searching.
B+ trees are multilevel structures containing a root node with entries pointing to the next lower level of nodes in the trees. The lowest level in the B+ tree holds the "leaf" pages, or blocks. This level of the tree (sometimes called the "sequence set") is actually a dense index to every row in the referenced table because it contains every indexed data value and its corresponding row ID (RID) or tuple identifier.
The RID references the page and location within the page for the relevant row. Often, leaf pages are chained to enable efficient data retrieval based on ordering, including range queries ("find all employees with salaries between $50,000 and $100,000") as well as queries requiring sorts. Figure 1 illustrates this structure.
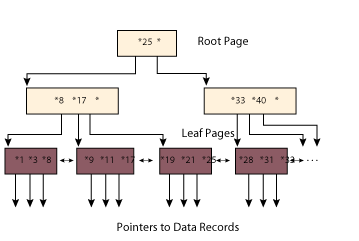
An important aspect of B+ tree indexes is that the distance between the root and each leaf node is the same and remains constant despite insertions and deletions of entries. This uniformity prevents skewing of levels and nodes on the tree. As a result, the tree remains balanced. Scanning the tree to access a particular leaf page will take about the same amount of time as accessing any other leaf page regardless of the key value being searched in the index.
B+ trees also tend to grow "wide" faster than "deep." Since traversing each level of the tree can cause an additional page or block access, it is more desirable when B+ trees grow wide (with lots of branches per level) faster than they grow deep. This type of growth enables the DBMS to add many index entries while still minimizing access time. The B+ tree structure is designed with this growth in mind.
In some cases, indexes alone can be used to satisfy a work request (or query), enabling the DBMS to save time by not retrieving the actual data pages associated with a table. This saving occurs if a query involves only the indexed columns. For example, if someone wanted a list of all item numbers greater than 1,000 and an index had been created on that column, the DBMS could retrieve this information by scanning the index, which typically requires much less time than searching the database.
VENDOR IMPLEMENTATIONS
Vendors have implemented various techniques to ensure that their B+ tree
indexes are efficient. For example, Version 4 of DB2/MVS introduces a "Type
2" B+ tree index that preserves the integrity of write transactions
for serialization of write activities without locking index pages. In addition,
suffix truncation helps minimize the key data stored at the nonleaf levels,
potentially reducing the number of index levels and related I/O activities.
At the leaf level of nonunique indexes, RIDs for duplicate values are stored
in ascending order, which can speed processing for delete and update operations.
Tandem's NonStop SQL/MP employs a somewhat unusual treatment of secondary indexes. Alternate indexes contain not only values for the index key but also for the table's primary key. Thus, a secondary index on the JOBTITLE column of the EMPLOYEE table would contain JOBTITLE data values and also data values for EMPNO, the EMPLOYEE table's primary key. A query involving employee numbers and job titles could be satisfied just by scanning the alternate index.
INDEX QUERY RESOLUTION
Several RDBMSs have enhanced their use of indexes with index AND and index
OR processing. These techniques (also used by several prerelational, inverted
list systems) are designed to resolve the logic of the query prior to searching
the database itself. That is, the Boolean logic in query predicates, consisting
of ANDs and ORs, is processed against the indexes prior to accessing the
database.
This processing against indexes filters index references to candidate rows so that all and only those rows required to satisfy the query are accessed directly. Such an approach offers performance benefits for certain types of queries.
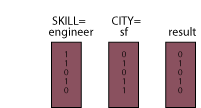
Consider an EMPLOYEE table with attributes for employee skills and city locations with indexes on each of these columns. These indexes might contain the entries such as the ones shown in Figure 2.

Now consider a query to retrieve data on employees who are engineers and
whose location is Newark. Without index query resolution capability, an
RDBMS would use (at most) one of these indexes-perhaps the index on skill-to
retrieve just the rows for employees who are engineers. Next, it would check
the city column of each retrieved row to determine which had a "Newark"
value and return it to the requesting application.
Notice that only one of the three retrieved rows satisfies both terms of the Boolean predicate. The two rows that do not qualify were accessed needlessly. (The reader can see that similar needless processing occurs when just the CITY index is used.) The I/O costs associated with this unnecessary processing will be substantial for databases of serious sizes.

As shown in Figure 3, these costs are avoided with the following index AND
processing logically described here:
1. The SKILL index is used to retrieve three employee index entries where SKILL = "engineer" (into temporary table T1), and the CITY index is used to retrieve employee index entries where CITY = "Newark" (into temporary table T2).
2. The intersection of T1 and T2 yields RIDs for all and only those employees who are engineers and are located in Newark.
BITMAP INDEXING REVISITED
The increased focus on complex queries for data warehousing and OLAP has
resulted in a revival of interest in bitmap indexes-an indexing approach
with a long history. Several DBMS vendors, including Red Brick Systems,
Sybase, and Oracle, have recently introduced bitmap indexing in support
of complex query.
Some prerelational DBMSs, notably Praxis International's (formerly Computer Corp. of America) Model 204, use bitmaps as "fast index" to data. The basic idea behind a bitmap is to use a single bit (instead of multiple bytes of data) to indicate that a specific value of an attribute is associated with an entity. For example, instead of storing eight characters to record "engineer" as the skill of a particular employee, this skill value is attributed to the employee by using a single bit. The relative position of the bit within the string of bits (or bitmap) is then mapped to the relevant employee's RID.
An obvious advantage of this technique is the potential for dramatic reductions in storage overhead. Consider a table with four million rows. A bitmap indicating which of these rows are for engineers requires about 500KB.
More importantly, the reduction in the size of index "entries" means that the index can sometimes be processed with no I/O and, more often, with substantially less I/O than would otherwise be required. In addition, many index-only queries (queries whose responses are derivable through index scans without searching the database) can benefit considerably. Finally, you can use low-level Boolean logic operations at the bit level to perform predicate evaluation at increased machine speeds. Of course, the combination of these factors can result in better query performance.
A potential drawback of bitmaps involves locking. Because a page in a bitmap contains references to so many rows, changes to a single row inhibit concurrent access for all other referenced rows in the index on that page.
The implementation of a bitmap index structure can take several forms, but at a conceptual level you can think of the index as a bit matrix. Figure 4 shows such a bit matrix for employee skills and locations. Skill codes are P for "programmer," C for "consultant," E for "engineer," and M for "manager." This index includes columns for two cities, San Francisco (SF) and New York (NY).

Because the skill attribute has four possible values in this example, four
bit positions are used to represent the particular skill value of each entity.
In general, n bits are required for n possible values of an
attribute.
When n is large for an attribute, the bit matrix will be sparsely populated and can include large clusters of zeros. For this reason, this structure is best reserved for use with attributes where n is small. The "optimal" number of values is an important database design decision.
Notice also that this example assumes that each employee has just one skill. (The association between an entity identifier and attribute is many-to-one.) This design also contributes to a sparsely populated matrix. You can achieve more effective use of space when multiple skill values can be associated with each employee (or when the associations are many-to-many). In any event, some implementations of bitmap indexes use special techniques for dealing with this clustering problem.
SAMPLE BITMAP INDEX PROCESSING
An indication of the index search speeds possible with bitmaps is given
by a query requiring the list of RIDs for employees with the "engineer"
skill. This query's index search uses Boolean mask operations at the bit
level to determine which bits are "on." These operations can be
executed extremely fast using 32 or 64 bits.
To retrieve those engineers located in San Francisco, low-level Boolean AND operations are applied to the bitmaps for E and SF. The result of these AND operations is the bitstring shown in the RESULT bitmap in Figure 5.
Some implementations avoid storing RIDs as a part of the bitmap index. Instead,
a simple mapping function is used to correlate bit positions in the bitmap
with RIDs. Patrick O'Neil has described one implementation of a bitmap index
that uses either hashed or B+ tree access to the bitmap for a particular
index entry.
For B+ tree access, the location of the relevant bitmap is in the leaf pages. The bitmaps (which correspond to the columns of the matrix in Figure 4) are segmented into multiple pages. One or more pages are used for each bitmap, and each bitmap shows whether or not a single value of an attribute is associated with each entity.
Thus, if the page size accommodates a string of 40,000 bits, then a single page will show whether or not each of 40,000 rows has one of the specific indexed values for the SKILL column of the employee table. Of course, this does not take into account any space overhead associated with the page. Roughly speaking, the page count of pages required for a given attribute/value pair depends on the page size as well as the cardinality of the table:
cardinality of indexed table / number of bits per page = page count per bitmap
And the total number of pages theoretically required to index all values of an indexed column is:
page count per bitmap 3 number of actual values =
total pages per indexed column
As the number of values per column increases, the problem of clustering becomes more pronounced. O'Neil describes two techniques that address this problem.
The first is a relatively straightforward technique for zero compaction. A count of succeeding consecutive zeros replaces such a zero cluster. In addition, if the system stores rows sorted on the key value (for example, the values for SKILL), then the bitmap for SKILL = "engineer" will cluster bits contiguously. Entire pages for remaining rows would consist exclusively of zero clusters.
The reference to the bitmap for the indexed value "engineer" indicates that all other rows that would normally be represented in the bitmap for this skill value are zeroes. Thus, no pages need be allocated for them and they need not be read during index processing. (The reader can consult the references for additional refinements of the implementation approach O'Neil describes.)
JOIN INDEXES
Complex queries against relational databases frequently require joining
rows from multiple tables. Providing good performance for queries that require
multitable joins of large tables has been an ongoing challenge to RDBMS
architects. Several methods are currently used to provide acceptable join
performance. These methods include nested loop, hash, sort/merge, and hybrid
joins.
A new method of optimizing join processing especially useful for complex queries makes use of join indexes. Again, the particular implementation of join indexes can vary.
First, a join index can be viewed as a "precomputed" join. That is, the index consists of references to those rows in two (or more) tables that satisfy the join condition. These references are joined in the index. Thus, the index might be viewed as a relation or table itself. The rows of the table consist entirely of such references, which are the RIDs of the relevant rows.
The index is created by identifying in advance those rows from the candidate join tables that satisfy the join condition. This processing occurs when the candidate tables are loaded and when subsequent insert operations against these tables occur. Figure 6 shows the join index generated from two candidate tables, DEPT and EMP, when the join condition is DEPT.city = EMP.city. (RIDs are depicted as part of the rows of each table for easy reference.)

The join index in this example is clustered on Drids (the RIDs from the
DEPT table) to facilitate access to rows from DEPT that participate in the
join. A second join index might be clustered on erids to facilitate access
to the EMP table's participating rows. A join with no additional filter
specified in an SQL WHERE clause is performed simply by processing the join
index sequentially to access and concatenate DEPT and EMP rows.
Use of a B+ tree index on the join index itself can enhance join processing of only those rows of DEPT that are qualified in a query by an SQL WHERE clause. For example, an index on DEPT.budamt would use the B+ tree index to facilitate processing a query requiring the join of just those departments whose budget amount is greater than $100,000 with rows in the EMP table.
Join indexes aren't limited to two-table joins. Indeed, they can support joins involving several tables and enhance processing of such joins considerably.
COMBINING INDEXES
The use of bitmaps to represent entries in a join index has been described
by O'Neil and Goetz Graefe. For each row of an outer table, an index entry
containing a bitmap references those rows of the inner table that satisfy
the join condition.
Two tables, CUSTOMER and FACT, are shown in Figure 7. Consider a query for the customer names (CNAME) from the CUSTOMER table and quantities ordered (QTY) from the FACT table for those customers living in San Francisco. This query involves a restriction of CUSTOMER rows where CCITY values are SF followed by the join of rows in the FACT table on cust# with the rows for San Francisco customer. The join index entries in Figure 7 represent the prejoin of FACT.cust# and CUST.cust#.
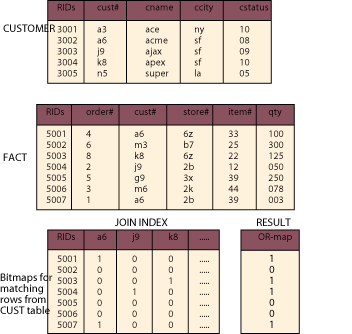
Application of Boolean OR operations on these three bitmap entries indicates
which rows from the FACT table share a common value on the join column (cust#)
with the rows restricted from the CUSTOMER table on SF. That is, they show
which rows for San Francisco customers from the FACT table must be joined
with rows from the CUSTOMER table in order to satisfy the query. The result
of the Boolean OR operations are shown in the bitmap labeled RESULT.
SPEEDING UP STAR JOINS
To preserve the tabular format of relational databases, many database designers
advocate the use of a star schema for multidimensional queries. Simply,
the star schema structures data into a detail table and multiple dimension
tables, each of which shares at least one attribute with the detail table.
As shown in Figure 7, the detail FACT table shares cust# (as a foreign key) with the primary key (cust#) of the CUSTOMER dimension table. The star schema typically includes several dimension tables, each of which shares an attribute with the detail table. Often, multidimensional queries require multitable joins involving several dimension tables with the detail table.
Imagine that this sample database includes multiple dimension tables, such as one for STORES with a primary key of store#. Then we could easily formulate a multidimensional query that (logically) requires the following processing:
1. Join of CUSTOMER and FACT on cust# into RESULT.
2. Join of RESULT and STORE on store#.
Assuming the availability of additional join indexes in bitmap form that show matching store numbers in the FACT and STORE tables, OR logic processing (similar to the OR logic processing already described for the CUSTOMER and FACT rows) will produce an OR-RESULT bitmap that shows rows from these two tables that share common store numbers (store#).
When this OR-RESULT bitmap and the OR-RESULT bitmap for the CUSTOMER and FACT table are ANDed together, the resulting bitmap will show those rows from the FACT table that would have been included as the result of a multitable join of the CUSTOMER, FACT, and STORE tables. Often, detail tables in a star schema (such as the FACT table) are very large, so the improvement in I/O and CPU time can be quite substantial.
R-TREES
R-trees are one type of index designed to support searches of spatial data,
which has multidimensional characteristics. In the geographic domain, objects
such as points, lines, and polygons may be used to represent the locations
of retail stores, roads, land parcels, zip code regions, or other entities
with 2D or 3D properties. Data about the location of such objects is usually
tracked through x, y or x, y, z coordinates.
Using R-tree indexes-or any of a number of other indexes designed for spatial data-is one means of enabling a DBMS to efficiently answer queries such as, "Show me the locations of all ACME grocery stores in this county," or "Show me all competing grocery stores within 10 miles of this vacant building."
Effective support of such queries can be important to a variety of applications. For example, conducting effective market research in certain industries may involve determining patterns-such as customer buying preferences-that are driven, in part, by geographic or spatially referenced data. Combining geographic data with traditional business data-such as area demographics and product sales data-can help market researchers visualize and detect such patterns that may be otherwise difficult to ascertain.
Thus, DBMS support for spatial data can be important for a variety of business applications, and R-trees represent one means of enabling a relational or object/relational DBMS to support queries involving such data. Use of R-trees (or other types of indexes geared toward spatial data) is relatively new in the commercial RDBMS arena. Illustra, recently acquired by Informix, uses R-trees in its 2D and 3D Spatial DataBlades.
What are R-trees? They are extended B-trees, adapted for handling points or regions. Like B-trees, they feature a balanced multilevel tree structure (with intermediate and leaf nodes). In other words, all leaf nodes exist at the same level, which is a desirable feature.
However, some of the information stored in R-tree indexes differs from what is stored in B-trees. In addition to storing a row or object identifier in leaf-level records, R-trees also store boundary data for the indexed object. In a 2D space, this approach would involve storing x and y coordinates of the lower-left and upper-right corners of the smallest possible rectangle-sometimes referred to as the "minimum bounding" rectangle-that encloses the indexed object. Intermediate levels contain pointers to lower-level nodes, as well as information about the minimum bounding rectangles that enclose objects stored at these nodes.
This idea may be new to many readers, so some explanation is in order. Figure 8 illustrates six sample 2D objects stored in a database. These objects are represented by rectangles A-F. (Circles, triangles, and other objects can also be indexed by constructing a minimum bounding rectangle that would enclose each.)
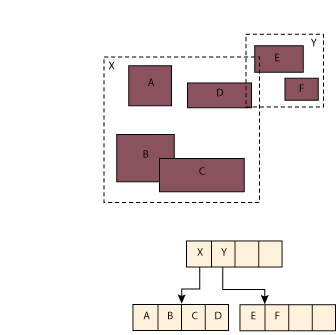
Information about these rectangles is stored in records at the index's leaf
level. In this case, the index's intermediate level contains two records:
one for rectangle X, which fully encloses the data objects A-D, and one
for rectangle Y, which fully encloses rectangles E and F.
Consider what might occur if an application identified a spatial region it wanted to query. In a graphics-based environment, someone could use a mouse to "draw" a polygon or circle on a map appearing on the screen. The envelope or minimum bounding rectangle for this area would be computed (if necessary) and used to enable an index search of other geographic objects (stored in the database) that fall within this region. Such a process could be useful for a variety of spatial queries, such as locating all the recreational facilities within a certain region surrounding a hotel.
TUNING FOR SPEED
Proper use of indexes can help speed access to data and significantly improve
performance of certain workloads. It's important to understand the different
types of indexing technology incorporated into commercial products because
some are better suited to different types of applications than others.
B+ trees are most widely applicable to general database applications and so are the most important indexing technology for many RDBMS users to learn. Some vendors also support other indexing technologies for special needs, such as bitmap and join indexes for certain complex queries or R-trees for spatial analysis.
These-and other-index technologies offer users one potential means of speeding access to data. Proper use of indexes can help users improve the performance of their DBMSs, especially when combined with tuning efforts that focus on other aspects of their environment, such as concurrency control, query optimization, and resource utilization.